机器学习基础

主要任务

• 分类（classification）：将实例数据划分到合适的类别中。
  • 应用实例：判断网站是否被黑客入侵（二分类 ），手写数字的自动识别（多分类）
• 回归（regression）：主要用于预测数值型数据。
  • 应用实例：股票价格波动的预测，房屋价格的预测等。

监督学习（supervised learning）

必须确定目标变量的值，以便机器学习算法可以发现特征和目标变量之间的关系。在监督学习中，给定一组数据，我们知道正确的输出结果应该是什么样子，并且知道在输入和输出之间有着一个特定的关系。 (包括：分类和回归)

非监督学习（unsupervised learing）

在机器学习，无监督学习的问题是，在未加标签的数据中，试图找到隐藏的结构。因为提供给学习者的实例是未标记的，因此没有错误或报酬信号来评估潜在的解决方案。

强化学习

这个算法可以训练程序做出某一决定。程序在某一情况下尝试所有的可能行动，记录不同行动的结果并试着找出最好的一次尝试来做决定。 属于这一类算法的有马尔可夫决策过程。

机器学习过程

算法汇总

机器学习 使用

选择算法需要考虑的两个问题

1. 算法场景
   • 预测明天是否下雨，因为可以用历史的天气情况做预测，所以选择监督学习算法
   • 给一群陌生的人进行分组，但是我们并没有这些人的类别信息，所以选择无监督学习算法、通过他们身高、体重等特征进行处理。
2. 需要收集或分析的数据是什么

选择算法图

机器学习 开发流程

1. 收集数据: 收集样本数据
2. 准备数据: 注意数据的格式
3. 分析数据: 为了确保数据集中没有垃圾数据；
   • 如果是算法可以处理的数据格式或可信任的数据源，则可以跳过该步骤；
   • 另外该步骤需要人工干预，会降低自动化系统的价值。
4. 训练算法: [机器学习算法核心]如果使用无监督学习算法，由于不存在目标变量值，则可以跳过该步骤
5. 测试算法: [机器学习算法核心]评估算法效果
6. 使用算法: 将机器学习算法转为应用程序

深度学习中激活函数的优缺点

为什么要使用非线性激活函数？

答：如果不使用激活函数，这种情况下每一层输出都是上一层输入的线性函数。无论神经网络有多少层，输出都是输入的线性函数，这样就和只有一个隐藏层的效果是一样的。这种情况相当于多层感知机(MLP)。

激活函数

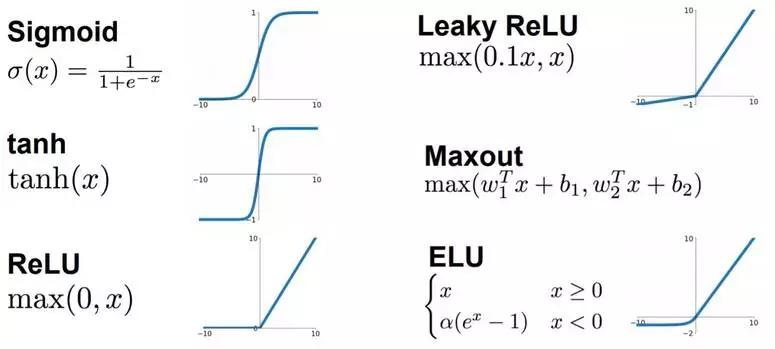
1. Sigmoid函数

sigmoid函数

x =  np.arange(-10,10,0.01)
y=1/(1+np.exp(-x))

#sigmoid函数图像
plt.plot(x,y,label='sigmoid函数图像')
plt.grid(color='b',linewidth='0.1' ,linestyle='--')

sigmoid的导数

#sigmoid导数图像
dev_y = y*(1-y)
plt.plot(x,dev_y,label='sigmoid导数图像')
plt.grid(color='b',linewidth='0.2' ,linestyle='--')

优点：

1. 便于求导的平滑函数；
2. 能压缩数据，保证数据幅度不会有问题；
3. 适合用于前向传播。

缺点：

1. 容易出现梯度消失（gradient vanishing）的现象：当激活函数接近饱和区时，变化太缓慢，导数接近0，根据后向传递的数学依据是微积分求导的链式法则，当前导数需要之前各层导数的乘积，几个比较小的数相乘，导数结果很接近0，从而无法完成深层网络的训练。
2. Sigmoid的输出不是0均值（zero-centered）的：这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。以 f=sigmoid(wx+b)为例， 假设输入均为正数（或负数），那么对w的导数总是正数（或负数），这样在反向传播过程中要么都往正方向更新，要么都往负方向更新，导致有一种捆绑效果，使得收敛缓慢。
3. 幂运算相对耗时

2. tanh函数

tanh函数

x =  np.arange(-10,10,0.01)
y=(np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))


#tanh函数图像
plt.plot(x,y)
plt.grid(color='b' , linewidth='0.1' ,linestyle='--')

tanh导数

#tanh导数图像
dev_y=1-np.square(y)
plt.plot(x,dev_y)
plt.grid(color='b' , linewidth='0.1' ,linestyle='--')

tanh函数将输入值压缩到 -1~1 的范围，因此它是0均值的，解决了Sigmoid函数的非zero-centered问题，但是它也存在梯度消失和幂运算的问题。

其实 tanh(x)=2sigmoid(2x)-1

3. ReLU(Rectified Linear Unit 修正的线性单元)

ReLU

x =  np.arange(-10,10,0.01)
y=list(map(lambda x:x if x>0 else 0,x))

#ReLU函数图像
plt.plot(x,y)
plt.grid(color='b' , linewidth='0.1' ,linestyle='--')

ReLU函数导数

#ReLU函数导数图像
dev_y =list(map(lambda x: 1 if x>0 else 0,x))
plt.plot(x,dev_y)
plt.grid(color='b' , linewidth='0.1' ,linestyle='--')

优点：

1. SGD算法的收敛速度比 sigmoid 和 tanh 快；（梯度不会饱和，解决了梯度消失问题）
2. 计算复杂度低，不需要进行指数运算；
3. 适合用于后向传播。

缺点：

1. ReLU的输出不是zero-centered；
2. Dead ReLU Problem（神经元坏死现象）：某些神经元可能永远不会被激活，导致相应参数永远不会被更新（在负数部分，梯度为0）。产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。 解决方法：采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
3. ReLU不会对数据做幅度压缩，所以数据的幅度会随着模型层数的增加不断扩张。

4. Leakly ReLU函数

Leakly ReLU函数

x =  np.arange(-10,10,0.01)
lambda1=0.1   #指定lambda为0.1
y=list(map(lambda x:x if x>0 else lambda1*x,x))


#leaky ReLU函数图像
plt.plot(x,y)
plt.grid(color='b' , linewidth='0.1' ,linestyle='--')

Leaky ReLU函数导数

#leaky ReLU函数导数图像
dev_y = list(map(lambda x: 1 if x>0 else lambda1,x))
plt.plot(x,dev_y)
plt.grid(color='b' , linewidth='0.1' ,linestyle='--')

用来解决ReLU带来的神经元坏死的问题，可以将0.01设置成一个变量a，其中a由后向传播学出来。_但是其表现并不一定比ReLU好_。

5. ELU函数（指数线性函数）

ELU函数（指数线性函数）

x =  np.arange(-10,10,0.01)
y=list(map(lambda x:x if x>0 else (np.exp(x)-1),x))

# ELU函数（指数线性函数）图像
plt.plot(x,y)
plt.grid(color='b',linewidth='0.1' ,linestyle='--')

ELU函数（指数线性函数）导数

# dev_y = list(map(lambda x: 1 if x>0 else lambda1,x))

# ELU函数（指数线性函数）图像
# plt.plot(x,dev_y)
# plt.grid(color='b',linewidth='0.1' ,linestyle='--')

ELU有ReLU的所有优点，并且不会有 Dead ReLU问题，输出的均值接近0（zero-centered）。但是计算量大，其表现并不一定比ReLU好。。

6. softmax

softmax

import math

z = np.arange(-10, 10, 0.05)
exp_z = [math.exp(z) for z in z]
sum_exp_z = sum(exp_z)
softmax_z = [round(i / sum_exp_z, 6) for i in exp_z]
plt.plot(z, softmax_z)
plt.grid(color='b',linewidth='0.1' ,linestyle='--')

多分类任务，当类别数k＝2时，Softmax回归退化为Logistic回归。

优化器

https://zhuanlan.zhihu.com/p/32626442

损失函数

https://zhuanlan.zhihu.com/p/60302475